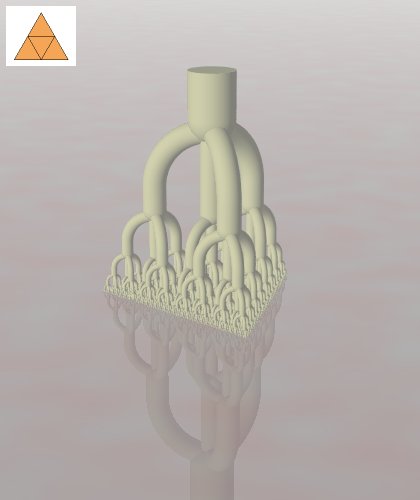
A fork fractal is built by putting smaller fork fractals together using a fork shaped joint. And then repeat this again and again.

The construction can be more precisely described by introducing an "R-shape" - a polygon that consists of small copies of itself. You take 2 R-shapes and place them above each other with the fork shaped joint between them. What you have now is a fork fractal of depth 1. It is the building block for the whole fractal.

To move on you take some building blocks and scale them down, so their upper R-shapes fit the lower R-shapes in the fractal built so far. In this way you build a layer in the bottom of the fractal, and its depth is increased by 1. This is repeated infinitely. But even when the depth becomes infinite the height of the fractal will stay finite. That is due to the inherent scaling of R-shapes. So you end up with a fork fractal, that is contained in a prism capped by the R-shapes.

For the fork fractal in the start of this article, the R-shape is like a piece of paper in A4 format. When it is halved it becomes 2 pieces in A5 format (which is just a smaller version of the A4 format). If A5 is halved you get 2 pieces of A6, et cetera.

I have invented the fork fractals myself. They probably have more artistic than mathematical relevance.

Variations

The R-shape determines basically how the fork fractal is put together. Fork fractals with the same R-shape can vary in height, thickness and the like - but their structure will be the same.

The R-shape can be split into more than 2 parts - it can be split into 3 parts.

The R-shape can be split into 4 parts.

The R-shape can be split into 5 parts.

Et cetera... This way to split rectangles tells us that there are infinitely many different fork fractals, because you can make an R-shape for every integer greater than 1.

Other R-shapes

There are lots of other R-shapes. For example a regular triangle split into 4 parts.

The R-shape can be a square split into 4 parts.

This article does not show all the R-shapes that exists. R-shapes is what mathematicians call "rep-tiles", and there is as far as I know noone that has a complete list of them. The illustration below shows some of the R-shapes ("rep-tiles") that I haven't made fork fractals for.

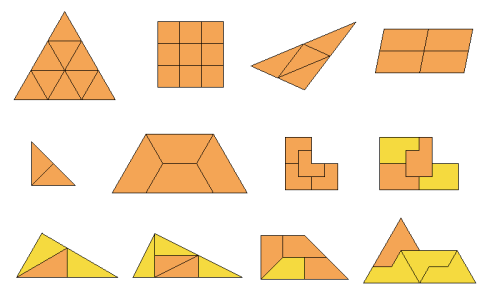
If you have a finite depth fork fractal, it is interesting to look at its "footprint" - the figure you will get if you put ink on the bottom of the fractal and press it down on a plane surface. The footprint consists of a lot of small copies of the footprint at depth 0. Below here are the footprints for the quadratic R-shape and the depths 0, 1, 2...

The scaling inherent in the R-shapes makes the footprint area the same for any depth. The larger the depth becomes, the more this area is spread out over the original R-shape.

Sierpinski R-shapes

If you cheat a little, and allow the R-shape to be a non-polygon, you can use Sierpinski fractals.

The R-shape can be a Sierpinski Triangle.

The R-shape can be a Sierpinski Carpet.

With these Sierpinski R-shapes the footprint area will reduce when the depth increases. If the depth is infinite the footprint area is 0 (zero).

Pseudo fork fractals.

Another way to cheat gives another variant, which carries the "branches" unchanged to the next depth, and adds new according to a special type of R-shape. For these fractals the footprint area will increase as the depth increases. Below here are a pair of examples

To form an idea of many simultanous processes, even though there is an inner connection between them and they supplement each other, exceeds human ability. [...] The symmetriad is a million, a billion, rather, raised to the power of N: it is incomprehensible. [...] We know, but cannot grasp, that above and below, beyond the limits of perception or imagination, thousands and millions of simultaneous transformations are at work, interlinked like a musical score by mathematical counterpoint. It has been described as a symphony in geometry, but we lack the ears to hear it.

from Solaris by Stanislaw Lem