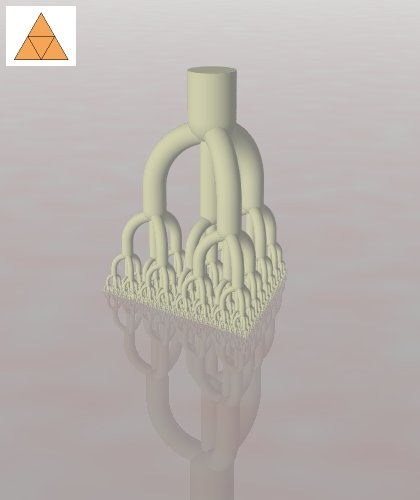
En gaffel-fraktal konstrueres ved at sætte mindre gaffel-fraktaler sammen med et gaffelformet samlestykke. Og så gentage det igen og igen.

Konstruktionen kan beskrives mere præcist ved at indføre en "R-form" - en polygon, som består af små kopier af sig selv. Man tager 2 R-former og placerer dem over hinanden med det gaffelformede samlestykke imellem. Det man har nu er en gaffel-fraktal med dybde 1. Den er byggestenen for hele fraktalen.

For at komme videre tager man nogle byggesten og formindsker dem, så deres øverste R-former passer ind i de nederste R-former i den fraktal man har bygget indtil nu. På denne måde bygger man et lag i bunden af fraktalen, og dens dybde øges med 1. Dette kan gentages i det uendelige. Men selv når dybden bliver uendelig vil fraktalens højde fortsat være endelig. Det skyldes den måde R-former skalerer byggesten på. Så man ender med en gaffel-fraktal, der er indeholdt i et prisme med R-formerne som endestykker.

For gaffel-fraktalen, der indledte denne artikel, svarer R-formen til et stykke papir i A4-format. Når det deles lige over bliver det til 2 stykker i A5-format (som jo bare er en mindre udgave af A4-formatet). Deles A5 fås 2 styk A6, og så videre.

Gaffel-fraktalerne er noget jeg selv har fundet på. De er nok mere kunstnerisk end matematisk interessante.

Variationer

R-formen bestemmer grundlæggende hvordan gaffel-fraktalen er skruet sammen. Gaffel-fraktaler med samme R-form kan variere i højde, tykkelse og lignende - men deres struktur vil være den samme.

R-formen kan deles i mere end 2 dele - den kan deles i 3 dele.

R-formen kan deles i 4 dele.

R-formen kan deles i 5 dele.

Og så videre... Denne måde at dele rektangler på fortæller os at der findes uendeligt mange forskellige gaffel-fraktaler, da man kan lave en R-form for hvert heltal større end 1.

Andre R-former

Der findes mange andre R-former. Eksempelvis en ligesidet trekant, som deles i 4.

R-formen kan være et kvadrat, som deles i 4.

Denne artikel viser ikke alle de R-former der findes. R-formerne er det som matematikere kalder "rep-tiles", og der er mig bekendt ingen der har en fuldstændig liste over dem. Illustrationen herunder viser nogle af de R-former ("rep-tiles") jeg ikke har lavet gaffel-fraktaler for.

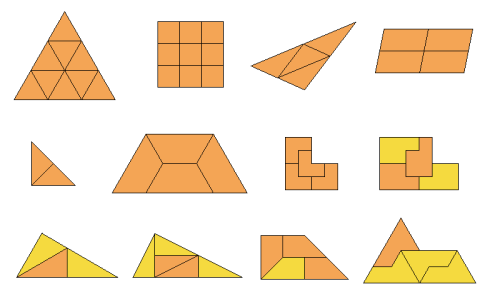
Har man en gaffel-fraktal med en endelig dybde, er det interessant at se på dens "fodaftryk" - den figur man vil få hvis man putter tryksværte på bunden af fraktalen og presser den ned på en plan overflade. Fodaftrykket består af en masse små kopier af fodaftrykket ved dybde 0. Herunder ses fodaftrykkene for den kvadratiske R-form og dybderne 0, 1, 2...

Den skalering der er indbygget i R-formerne, gør at fodaftrykkets areal er det samme i alle dybder. Jo større dybden bliver, jo mere bliver dette areal spredt ud over den oprindelige R-form.

Sierpinski-R-former

Hvis man snyder lidt, og tillader at R-formen ikke er en polygon, kan man bruge Sierpinski-fraktaler.

R-formen kan være en Sierpinski-trekant.

R-formen kan være et Sierpinski-tæppe.

Med disse Sierpinski-R-former vil fodaftrykkets areal mindskes når dybden vokser. Hvis dybden er uendelig, er fodaftrykkets areal 0 (nul).

Pseudo-gaffel-fraktaler

En anden måde at snyde på giver en anden variant, hvor "grenene" føres uændret med til næste dybde, og der tilføjes nye efter en særlig slags R-form. For disse fraktaler vil fodaftrykkets areal vokse med dybden. Herunder er et par eksempler.

At danne sig en forestilling af mange samtidigt forløbende processer, selv om der er en indre sammenhæng mellem dem og de supplerer hinanden, overstiger den menneskelige formåen. [...] Symmetriaden er selve uforståeligheden opløftet til potenser af millioner, nej af milliarder. [...] vi ved - vi ved det kun, men vi forstår det ikke - at der samtidig foregår omdannelser af samme art over og under os, i dybe afgrunde, hvor vort blik ikke kan trænge ned, og som vor fantasi ikke kan forestille sig; der kan være millioner af den slags processer i gang samtidigt - som noder forbundet med hinanden gennem matematikkens kontrapunkt. Helheden har været beskrevet som "en geometrisk symfoni"; men i så fald er vi døve tilhørere til den.

fra Solaris af Stanislaw Lem